Is That a Good Probability Score - the Brier Score Edition
 Sunday, December 22, 2013 at 7:19PM
Sunday, December 22, 2013 at 7:19PM In recent blogs about the Very Simple Ratings System (VSRS) I've been using as my Probability Score metric the Brier Score, which assigns scores to probability estimates on the following basis:
Brier Score = (Actual Result - Probability Assigned to Actual Result)2
For the purposes of calculating this score the Actual Result is treated as (0,1) variable, taking on a value of 1 if the team in question wins, and a value of zero if that team, instead, loses. Lower values of the Brier Score, which can be achieved by attaching large probabilities to teams that win or, equivalently, small probabilities to teams that lose, reflect better probability estimates.
Elsewhere in MAFL I've most commonly used, rather than the Brier Score, a variant of the Log Probability Score (LPS) in which a probability assessment is scored using the following equation:
Log Probability Score = 1 + log2(Probability Associated with Winning team)
In contrast with the Brier Score, higher log probabilities are associated with better probability estimates.
Both the Brier Score and the Log Probability Score metrics are what are called Proper Scoring Rules, and my preference for the LPS has been largely a matter of taste rather than of empirical evidence of superior efficacy.
Because the LPS has been MAFL's probability score of choice for so long, however, I have previously written a blog about empirically assessing the relative merits of a predictor's season-average LPS result in the context of the profile of pre-game probabilities that prevailed in the season under review. Such context is important because the average LPS that a well-calibrated predictor can be expected to achieve depends on the proportion of evenly-matched and highly-mismatched games in that season. (For the maths on this please refer to that earlier blog.)
WHAT'S A GOOD BRIER SCORE?
What I've not done previously is provide similar, normative data about the Brier Score. That's what this blog will address.
Adopting a methodology similar to that used in the earlier blog establishing the LPS norms, for this blog I've:
- Calculated the implicit bookmaker probabilities (using the Risk-Equalising approach) for all games in the 2006 to 2013 period
- Assumed that the predictor to be simulated assigns probabilities to games as if making a random selection from a Normal distribution with mean equal to the true probability - as assessed in the step above - plus some bias between -10% and +10% points, and with some standard deviation (sigma) in the range 1% to 10% points. Probability assessments that fall outside the (0.01, 0.99) range are clipped. Better tipsters are those with smaller (in absolute terms) bias and smaller sigma.
- For each of the simulated (bias, sigma) pairs, simulated 1,000 seasons with the true probabilities for every game drawn from the empirical implicit bookmaker probabilities for a specific season.
Before I reveal the results for the first set of simulations let me first report on the season-by-season profile of implicit bookmaker probabilities, based on my TAB Sportsbet data.
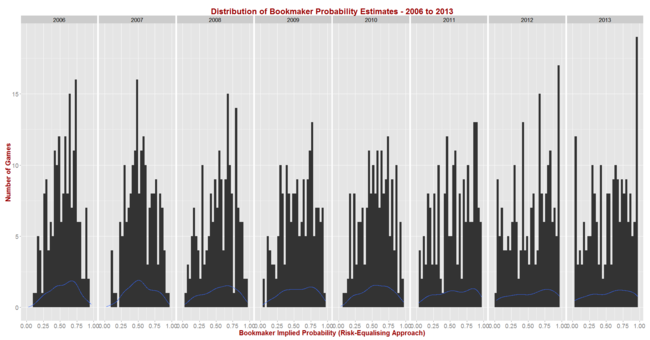 The black bars reflect the number of games for which the home team's implicit home team probability fell into the bin-range recorded in the x-axis, and the blue lines map out the smoothed probability density of that same data. These blue lines highlight the similarity in terms of the profile of home team probabilities of the last three seasons. In these three years we've seen quite high numbers of short-priced (ie high probability) home team favourites and few - though not as few as in some other years - long-shot home teams.
The black bars reflect the number of games for which the home team's implicit home team probability fell into the bin-range recorded in the x-axis, and the blue lines map out the smoothed probability density of that same data. These blue lines highlight the similarity in terms of the profile of home team probabilities of the last three seasons. In these three years we've seen quite high numbers of short-priced (ie high probability) home team favourites and few - though not as few as in some other years - long-shot home teams.
Seasons 2008, 2009 and 2010 saw a more even spread of home team probabilities and fewer extremes of probability at either end, though home team favourites still comfortably outnumbered home team underdogs. Seasons 2006 and 2007 were different again, with 2006 exhibiting some similarities to the 2008 to 2010 period, but with 2007 standing alone as a season with a much larger proportion of contests pitting relatively evenly-matched tips. That characteristic makes prediction more difficult, which we'd expect to be reflected in expected probability scores.
So, with a view to assessing the typical range of Brier Scores under the most diverse sets of conditions, I ran the simulation steps described above once using the home team probability distribution from 2013, and once using the distribution from 2007.
THE BRIER SCORE RESULTS
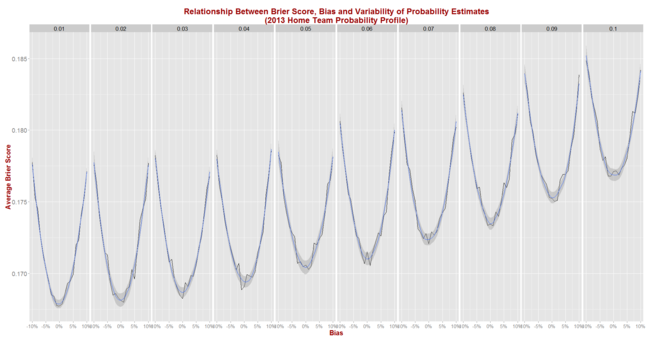
Here, firstly, are the results for all (bias, sigma) pairs, each simulated for 1,000 seasons that look like 2013.
As we'd expect, the best average Brier Scores are achieved by a tipster with zero bias and the minimum, 1% standard deviation. Such a tipster could expect to achieve an average Brier Score of about 0.167 in seasons like 2013.
For a given standard deviation, the further is the bias from zero the poorer (higher) the expected Brier Score and, for a given bias, the larger the standard deviation the poorer the expected Brier Score as well. So, for example, we can see from the graph that an unbiased tipster with a 5% point standard deviation should expect to record an average Brier Score of about 0.175.
Using Eureqa to fit an equation to the Brier Score data for all 210 simulated (bias, sigma) pairs produces the following approximation:
Expected Brier Score = 0.168 + 0.89 x Bias2 + 0.87 x Sigma2
This equation, which explains 98% of the variability in the average Brier Scores across the 210 combinations, suggests that the Brier Score of a tipster is about equally harmed by equivalent changes in percentage point terms in bias and variance (ie sigma squared). Every 1% point change in squared bias or in variance adds about 0.09 to the expected Brier Score.
Next, we simulate Brier Score outcomes for seasons that look like 2007 and obtain the following picture:
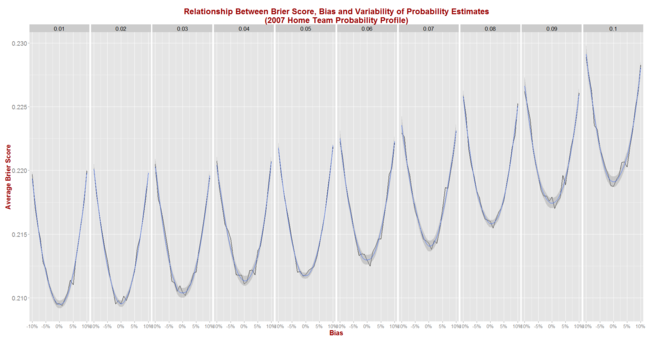 The general shape of the relationships shown here are virtually identical to those we saw when using the 2013 data, but the expected Brier Score values are significantly higher.
The general shape of the relationships shown here are virtually identical to those we saw when using the 2013 data, but the expected Brier Score values are significantly higher.
Now, an unbiased tipster with a 1% point standard deviation can expect to register a Brier Score of about 0.210 per game (up from 0.167), while one with a 5% point standard deviation can expect to return a Brier Score of about 0.212 (up from 0.175).
Eureqa now offers the following equation to explain the results for the 210 (bias, sigma) pairs:
Expected Brier Score = 0.210 + 0.98 x Bias2 + 0.94 x Sigma2
This equation explains 99% of the variability in average Brier Scores across the 210 combinations and, when compared with the earlier equation, suggests that:
- A perfect tipster - that is one with zero bias and zero variance - would achieve a Brier Score of about 0.210 in seasons like 2007 and of 0.168 in seasons like 2013
- Additional bias and variability in a tipster's predictions are punished more in absolute terms in seasons like 2007 than in seasons like 2013. This is evidenced by the larger coefficients on the bias and variance terms in the equation for 2007 compared to those for 2013.
In seasons in which probability estimation is harder - that is, in seasons full of contests pitting evenly-matched teams against one another - Brier Scores will tend to do a better job of differentiating weak from strong predictors.
THE LPS RESULTS
Though I have performed simulations to determine empirical norms for the LPS metric before, I included this metric in the current round of simulations as well. Electrons are cheap.
Here are the curves for simulations of LPS for the 2013-like seasons.
 Eureqa suggests that the relationship between expected LPS, bias and variance is, like that between Brier Score, bias and variance, quadratic in nature, though here the curves are concave rather than convex. We get:
Eureqa suggests that the relationship between expected LPS, bias and variance is, like that between Brier Score, bias and variance, quadratic in nature, though here the curves are concave rather than convex. We get:
Expected LPS = 0.271 - 4.68 x Bias2 - 4.71 x Sigma2
This equation explains 99% of the variability in average LPSs observed across the 210 combinations of bias and sigma.
Finally, simulating using 2007-like seasons gives us this picture.
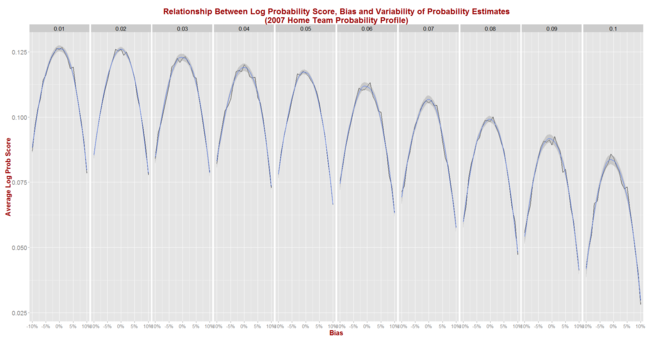 Again we find that the shape when using the 2007 data is the same as that when using the 2013 data, but the absolute scores are poorer (which here means lower).
Again we find that the shape when using the 2007 data is the same as that when using the 2013 data, but the absolute scores are poorer (which here means lower).
Eureqa now offers up this equation:
Expected LPS = 0.127 - 4.17 x Bias2 - 4.35 x Sigma2
This equation accounts for 97% of the total variability in average LPS across the 210 simulated pairs of bias and sigma and suggests that expected LPSs in seasons like 2007 are less sensitive to changes in bias and variance than are expected LPSs in seasons like 2013. This is contrary to the result we found for expected Brier Scores, which were more sensitive to changes in bias and variance in seasons like 2007 than in seasons like 2013.
In more challenging predictive environments, therefore, differences in predictive ability as measured by different biases and variances, are likely to result in larger absolute differences in Brier Scores than differences in LPSs.
SUMMARY AND CONCLUSION
We now have some bases on which to make normative judgements about Brier Scores and Log Probability Scores, though these judgements require some knowledge about the underlying distribution of true home team probabilities.
If 2014 is similar to the three seasons that have preceded it then a "good" probability predictor should produce an average Brier Score of about 0.170 to 0.175, and an average LPS of about 0.230 to 0.260. In 2013, the three bookmaker-derived Probability Predictors all finished the season with average LPS' of about 0.260.
[EDIT : It's actually not difficult to derive the following relationship theoretically, which holds where the truncation of probabilities at 1% and 99% is not necessary (ie for small bias, small sigma and probabilities near 50%)
Expected Brier Score = True Home Probability x (1 - True Home Probability) + Bias2 + Sigma2
The equations for Expected Brier Scores above have coefficients on Bias and Sigma that are less than 1 solely due to the effects of probability truncation, which tend to improve (ie lower) Brier Scores.
Deriving a similar equation theoretically rather than empirically for the Expected LPS of a contest is a far more complicated endeavour ...]

Reader Comments